électronique numérique: Comment obtenir une expression logique à partir d'une table de vérité ?

Le tableau de vérité est l'une des méthodes pour exprimer une fonction logique d'un circuit électronique numérique. L'objectif de la création d'un tableau de vérité est qu'il permet d'extraire l'expression algébrique booléenne ou l'équation logique du circuit numérique. Dans cet article, nous découvrirons toutes les méthodes qui permettent d'extraire l'expression algébrique à partir de n'importe quel tableau de vérité.

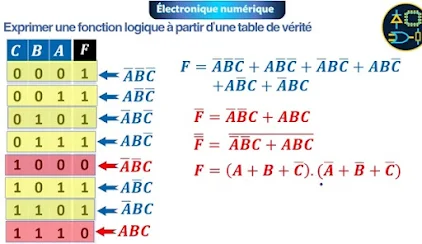
Exprimer une fonction logique à partir d'une table de vérité

Entrées		Sortie
A	B	F
0	0	0
0	1	1
1	0	0
1	1	0

Prenons le tableau ci-dessus comme exemple initial pour comprendre la méthode. Pour extraire l'équation algébrique à partir du tableau de vérité, nous posons toujours la question : quand la sortie est-elle égale à 1 ? Pour répondre à cette question, nous recherchons et identifions les lignes du tableau de vérité où la sortie est égale à 1.

Entrées		Sortie
A	B	F
0	0	0
0	1	1
1	0	0
1	1	0

Pour répondre à la question de savoir quand la sortie est égale à 1, nous examinons les valeurs booléennes que prennent les entrées dans la ligne où la sortie vaut 1. Dans notre exemple, nous avons F=1 lorsque A=0 ET B=1. Nous exprimons les états des entrées algébriquement par l'expression suivante : lorsque A=1, nous écrivons A, et lorsque A=0, nous écrivons Ā (A barre). La même règle s'applique à toutes les entrées.

F = A · B

Dans le deuxième exemple, dans le tableau ci-dessous, nous avons la sortie F égale à 1 dans plusieurs lignes. Ainsi, nous posons la même question : quand F est-il égal à 1 ? Nous répondons en examinant les valeurs prises par les entrées. Dans le tableau, il y a trois lignes où la sortie est égale à 1, et par conséquent, nous répondons en fonction de ces valeurs.

Entrées		Sortie
A	B	F
0	0	1
0	1	1
1	0	0
1	1	1

Nous disons donc que F=1 si A=1 ET B=1 OU A=0 ET B=0 OU A=0 ET B=0.

L'expression ET représente la porte logique AND, remplacée par le symbole (.). L'expression OU représente la porte logique OR, remplacée par le symbole algébrique (+). Ainsi, nous obtenons l'expression algébrique logique finale sous la forme suivante :

F = A.B + A.B + A.B

Nous passons maintenant au tableau de vérité avec trois entrées et prenons l'exemple suivant :

Entrées			Sortie
A	B	C	F
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Dans le tableau de vérité ci-dessus, la sortie F prend la valeur booléenne 1 dans trois lignes. Nous commençons par la première ligne où F=1 et nous examinons les valeurs des entrées. Comme nous l'avons mentionné, si une entrée a la valeur 1, nous écrivons le nom de l'entrée tel quel, et si elle a la valeur 0, nous l'écrivons avec une barre. Par exemple, pour l'entrée C, si elle vaut 1, nous écrivons C, et si C vaut 0, nous écrivons C̄ (C barre). La même règle s'applique aux autres entrées A et B.

Entrées			Sortie
A	B	C	F
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Dans le tableau de vérité, nous avons F=1 lorsque A=0, B=1 et C=1. Ainsi, nous écrivons Ā.B.C

Ensuite, dans la ligne suivante, nous avons F=1 lorsque A=1, B=0 et C=0. Ainsi, nous écrivons A.B.C.

Ensuite, dans la dernière ligne, nous avons F=1 lorsque A=1, B=1 et C=1. Par conséquent, nous écrivons A.B.C.

Ainsi, l'équation F qui représente la fonction logique dans ce tableau est :

F = A.B.C+A.B.C + A.B.C

Dans certains grands tableaux de vérité, la sortie F prend la valeur 1 dans de nombreuses lignes du tableau. Par conséquent, l'équation algébrique logique devient longue et nécessite un temps considérable pour être simplifiée.

Dans de tels cas, nous utilisons une autre méthode simplifiée qui nous permet d'obtenir rapidement une équation algébrique plus courte. Cette méthode consiste à extraire l'équation de F̅ (F barre) en identifiant les lignes où F=0, puis à inverser cette équation en utilisant les lois de De Morgan pour obtenir F.

Entrées				Sortie
A	B	C	D	F
0	0	0	0	1
0	0	0	1	1
0	0	1	0	1
0	0	1	1	1
0	1	0	0	1
0	1	0	1	0
0	1	1	0	0
0	1	1	1	1
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

Dans le tableau ci-dessus, nous avons un tableau de vérité avec quatre variables, et nous constatons que la sortie F est égale à 1 dans la plupart des lignes. Si nous appliquions la première méthode, l'équation algébrique serait très longue. Par conséquent, nous nous baserons sur les lignes où F=0, et nous remarquons qu'il n'y a que deux lignes. Ainsi, nous allons extraire l'équation de F̅ en posant la question : quand F est-il égal à 0 ?

Nous répondons donc que F=0 lorsque A=0, B=1, C=0 et D=1 OU A=0, B=1, C=1 et D=0.

F = A.B.C.D + A.B.C.D

Après avoir extrait l'équation de F̅, nous appliquons les lois de De Morgan pour obtenir F.

Nous pouvons extraire directement l'équation de F en utilisant les lignes où F=0, sans appliquer les lois de De Morgan. Cette expression algébrique est appelée la forme canonique "produit des sommes " (POS), qui est une expression d'une fonction logique où la sortie est le résultat d'une somme de produits.

Entrées			Sortie
A	B	C	F
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	0

Si nous voulons extraire l'expression de F à partir des lignes où F=0, nous posons la même question : quelles sont les valeurs des entrées pour que F soit égal à 0 ? Ainsi, F=0 si A=0 ou B=0 ou C=0. Dans ce cas, lors de l'écriture de l'expression algébrique, lorsque A=0, nous écrivons A, et lorsque A=1, nous écrivons Ā (A barre).

Ensuite, nous complétons la réponse en passant aux lignes suivantes où F=0, et nous disons que F=0 si A=1 ou B=1 ou C=0. Par conséquent, nous écrivons :